Les principes de la modélisation

Objectif des modèles numériques

La finalité des modèles numériques est de représenter schématiquement une entité ou un processus réel, dans le but de comprendre et d’expliquer son fonctionnement, mais également de prévoir son comportement.

En hydrogéologie, la modélisation numérique s’applique à retranscrire, à l’aide de la programmation informatique, l’écoulement des eaux souterraines et la migration des polluants dans le système aquifère  . La démarche de représentation théorique simplifiée d’un tel système comporte :

• la définition d’une structure (architecture ou géométrie des réservoirs),
• la formulation de lois (relations déterministes ou probabilistes) reliant les impulsions ou entrées du système à ses réponses ou sorties,
• la définition des paramètres (constants ou variables) entrant dans ces relations [1].

Les modèles numériques sont utilisés en tant que :

• outil de compréhension, parce qu’ils permettent d’inventorier l’ensemble des données disponibles sur un site d’étude et de comprendre son fonctionnement. A contrario, ils identifient les zones en déficit d’informations, qui pourront être investiguées et les zones à surveiller ;
• outil de gestion et de prédiction des ressources et/ou de la qualité des eaux. Les modèles servent à prédire l’influence d’un pompage, estimer l’impact d’aménagements (barrage, bâtiments…) sur les niveaux d’eau dans les nappes   et les débits dans les cours d’eau, prévoir l’évolution d’une pollution (trajectoires, temps de transfert, concentration) ou encore, à partir d’un modèle de gestion valide (ex. : Modèle Nord-Aquitain), aider à la définition de schéma de gestion et/ou évaluer les conséquences des changements climatiques sur les réserves en eau.

Les modèles intègrent diverses équations mathématiques qui sont communément résolues au moyen de deux méthodes [2] : la méthode des différences finies et la méthode des éléments finis. Dans les deux cas, la modélisation nécessite que le système aquifère   soit discrétisé (ou segmenté) en mailles (ou cellules) de formes variables.

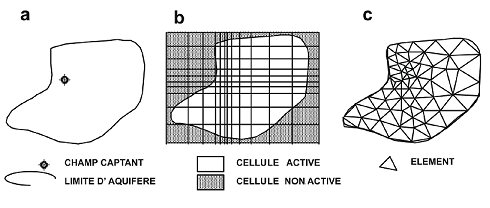
Figure 1 : Discrétisation d’un aquifère à l’aide d’un maillage en différences finies -b- et en éléments finis -c-

Le maillage en différences finies consiste en des cellules parallélépipédiques rectangulaires généralement cubiques mais des modifications permettent de resserrer le maillage au niveau d’une zone d’intérêt comme ici au droit du champ captant (figure 1-b).
Le maillage en éléments finis est représenté par des cellules polygonales quelconques (triangles, quadrilatères…) et offre donc plus de flexibilité dans la représentation d’un système irrégulier (figure 1-c).

Même si chaque approche a ses avantages et ses inconvénients, il y a très peu de problèmes hydrogéologiques pour lesquels l’une est clairement meilleure que l’autre [3]. Les méthodes se différencient notamment par les difficultés de programmation et les précisions numériques.

Exemple de modélisation d’un aquifère   en deux dimensions

Figure 2 : Représentation schématique d’un aquifère en deux dimensions

On souhaite simuler l’écoulement de l’eau dans un aquifère  , en deux dimensions, constitué d’une formation sableuse et d’une autre sablo-argileuse avec une épaisseur constante. Il est bordé d’un plan d’eau au nord-ouest et d’une rivière à l’est.
L’objectif est de retranscrire les hauteurs d’eau ainsi que les directions d’écoulement en chaque point de l’aquifère  .


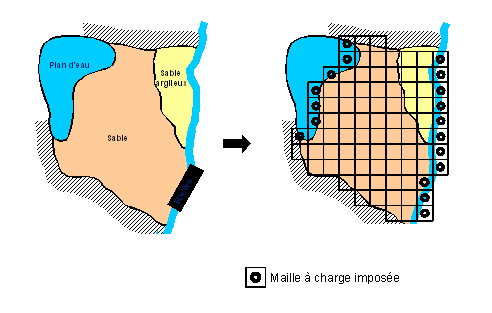
La méthode choisie est celle des différences finies. Le maillage retenu est donc rectangulaire et régulier (figure 3). Le nombre, et donc la taille des mailles, est défini selon la précision des résultats souhaitée, des contours du système à modéliser ou encore de la puissance de l’ordinateur (plus il y a de mailles et plus les temps de calculs seront longs).
Au sein de chaque maille, sont renseignées les propriétés hydrauliques de l’aquifère  , comme sa perméabilité  . Quand cela est possible, des valeurs d’infiltration (pluies efficaces) sont intégrées, parce qu’elles permettent de prendre en compte la recharge du système. Enfin, on renseigne les mailles où les niveaux piézométriques sont connus.

Dans notre exemple, on considère que l’altitude du plan d’eau est à un niveau piézométrique   (H) constant. Cette charge est dite imposée (elle n’est pas calculée par la suite et sert de référence). De la même façon, on simule la rivière dont on connait le niveau en amont et en aval. On applique une diminution linéaire entre ces deux points afin de renseigner la valeur du niveau de la rivière sur toutes les mailles recoupant son tracé.

Figure 3 : Création d’un maillage rectangulaire régulier représentant l’aquifère

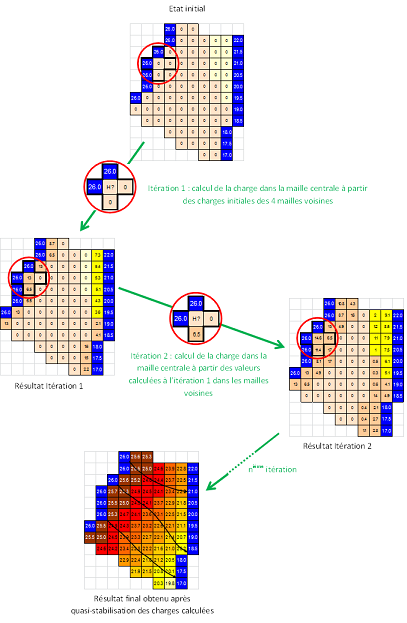
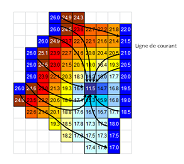
Le modèle va maintenant résoudre, pour chaque maille, l’équation de l’écoulement. Les calculs sont menés d’une maille à l’autre par approximation successive de manière itérative (figure 4). Ainsi, à partir des conditions initiales renseignées précédemment, les charges pour chaque maille sont calculées les unes après les autres plusieurs fois avec les charges des 4 mailles voisines (itération). Les itérations sont arrêtées lorsqu’une pseudo-stabilisation des charges calculées dans chaque maille est obtenue. Dans notre exemple, la répartition des charges ainsi calculée est obtenue après 300 itérations environ.

Figure 4 : Principe du processus itératif

Figure 5 : Simulation intégrant un pompage

De la même manière, la simulation d’un pompage (avec un débit de prélèvement   connu) est réalisable (figure 5).




La cohérence des calculs est ensuite vérifiée et le modèle validé, en confrontant les résultats obtenus à des observations faites directement sur le terrain (niveau piézométrique   d’un forage, d’une source, d’un cours d’eau).




Au final, une étude hydrogéologique à l’aide de l’outil numérique permet de rendre compte du fonctionnement d’un système relativement complexe. Cependant, compte-tenu des différents processus qui entrent en jeu (depuis le choix de la méthode de résolution jusqu’aux hypothèses simplificatrices introduites dans le modèle), une discussion de la pertinence de la modélisation pour le site à étudier est primordiale. De la même manière, la discussion et la critique des résultats obtenus sont obligatoires. En aucun cas, la modélisation ne peut se substituer au jugement humain.